
Natural Harmony: How did the Stonehenge Druids Measure the Landscape?
What were the Proto-Druids up to at Stonehenge? Advances in GPS technology and other sophisticated mapping software allow their prehistoric surveying activities to be investigated in ways that were virtually impossible before the 21st century. In this article I discuss their spectacular measuring and construction activities across the Stonehenge Neolithic landscape, circa 3,500 – 3,000 BC.
Background
I have been investigating British Prehistoric landscapes for some time and I believe that there were certain Neolithic people, whom I refer to as Proto-Druids, who were surveying their lands on a scale never fully appreciated before. To examine this phenomenon of measuring, I utilized GPS and other mapping software.
However, I realize that the reader will not have immediate access to such technology but one could still gain an appreciation of my forthcoming data by using both Ordnance Survey maps and Google Earth. And I will provide the necessary Ordnance Survey map coordinates to help you identify the key locations discussed here, so that you can check the measurements for yourself (see Table One).
Measuring the Landscape
My research proposes that around 3,500 BC, particular members of the Early Neolithic society, the Proto-Druids, were physically measuring vast areas of the landscape surrounding Stonehenge. Initially, they identified the highest hilltops within the immediate landscape and then they measured the distances between each one of them, as well as measuring the distance between them and the nearby River Avon. What is most striking about these surveying activities is that the Proto-Druids noticed a very unusual, mysterious observation concerning these “natural measurements”. Let me explain further.
Having identified the highest hilltop (High Point 1), the Proto-Druids then found the summit to be at a distance of 9,090 ft (2.77 km) between it and the second highest hilltop (High Point 2). Next, they measured the distance from High Point 1 towards the River Avon, travelling due east, and they found that measurement to also be 9,090 ft (2.77 km).

Fig.1. The Neolithic ritual landscape at Stonehenge
Furthermore, when they travelled 9,090 ft (2.77 km) due south from High Point 1, they came across a location locally known as Stonehenge Bottom. This is an unusual natural “dip” in the landscape and is, incidentally, the same area where a number of geological features converge. These form a series of natural ridges or gullies, identified by Stonehenge expert, Professor Mike Parker Pearson. In addition the same location holds the outlet for a spring where a small stream of water once flowed.
Astonishingly, it appears as if Mother Nature had planned the Stonehenge landscape to her own geometrical, harmonious scheme, which balanced the positions of the hills in relation to the river and other geological features, such as those gullies and springs. Even more astonishing is that Neolithic man managed to not only notice this harmonious scheme but also add to it. Indeed, between 3,500 and 3,000 BC, measurements equal or proportional to 9,090 ft (2.77 km) were then incorporated into the positioning of the monuments as well as their inherent dimensions.
This pattern of both the positioning and inherent dimensions can be seen in (at least) nine long barrows, two “cursuses” (systems of large trenches), one causewayed camp and four henges (See Fig. 1). Unfortunately, space prevents a full description of every one of those monuments identified here, so I shall use the Stonehenge’s Major Cursus as the main case study and then briefly mention Stonehenge.
Case Study - The Major Cursus at Stonehenge
Located half a mile north of Stonehenge is the barely recognizable remains of a prehistoric linear earthwork known as the Major Cursus (Fig.2). It dates to 3,500 BC and once consisted of a set of external parallel ditches, with internal banks that stretched out across a long but narrow strip of land. This earthwork is just one of many other similar cursuses found elsewhere across Prehistoric Britain and they all date to between 3,500 – 3,000 BC.
Within the Stonehenge landscape there are actually two cursuses (the Lesser Cursus and the Major Cursus). The name “Cursus” is of course an anachronism. This name was first applied back in the 18th century, when the antiquarian William Stukeley had a better view of the remains of the prehistoric Stonehenge Landscape. He concluded that it was an ancient Roman racetrack for chariot racing. Not a bad idea for a gentleman living in 1723.

Fig.2. The Major Cursus at Stonehenge.
As to what their functions were, these remain enigmatic. Moreover, what archaeology does come out of them tends to be limited to the antler bones they used as tools, to dig out the chalk and create the ditches and the inner earthen banks. Post holes have been found, but the practical role of sighting posts is as good as any other explanation for their presence. Even burials are at a distinct minimum, and where they do occur they tend to be found in those substantial earthen long barrows that generally abut the cursuses.
Still, there are interpretations ranging from the astronomical to the ritual. For instance, the Major Cursus at Stonehenge has been interpreted as a processional pathway, which guided people through the Stonehenge ritual landscape. Alternatively, the Major Cursus may function as part of a solar calendar, as it is orientated east-west and aligned with the Spring and Autumn Equinoxes – although not all cursuses are orientated in the same manner as this one.
Out of interest, why not take a quick walk with me along the Major Cursus and I will explain a few more ideas:
What is of particular importance here is the length of the Major Cursus. At its longest length, which has been surveyed by Robert Newall, it is 9,090 ft (2.77 km) long. I have also measured this Cursus using GPS and confirm it to be 9,090 ft (2.77 km). So, here we see a man-made repetition of the same 9,090 ft (2.77 km) measurement obtained from the natural landscape.
Coincidence, you may think. Not so, as my survey measurements will show in the following figures which have been complied not only within a margin of error of +/- 1 m (3 ft), but which also take into account the gradients and slopes of the land measured. Incidentally, I am not implying that the Neolithic communities were using either the Imperial or Metric systems of measurement, I am simply using these conventions for ease of explanation.
Measurement Commonalities in the Landscape
Fig. 3 shows how the 9,090 ft (2.77 km) measurement is found in multiple instances across the landscape. We see it between High Point 1 and High Point 2, between High Point 1 and Stonehenge Bottom, and between High Point 1 and the nearest point of the River Avon. Also shown in Fig.3 is the 9,090 ft (2.77 km) distance between High Point 1 and the Lesser Cursus. Additionally, the Lesser Cursus is exactly half this distance from High Point 4, that is at 4,545 ft (1.39 km).
Moreover, the same 9,090 ft (2.77 km) measurement also extends south-east from High Point 1 towards the geometrical center of the Neolithic Durrington Walls Henge. The 9,090 ft (2.77 km) measurement is then repeated again, south-west towards High Point 3, Coneybury Hill, upon which the Neolithic Coneybury Henge was built. Incidentally, note the intentional 90-degree angle between these last three features, suggesting extreme precision in land measuring!
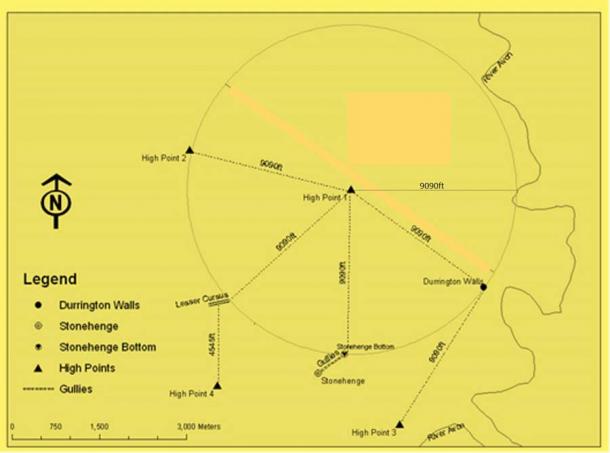
Fig.3. The 9090 ft “natural measurements” at Stonehenge.
Fig.4 shows how the Major Cursus forms an axis across this ritual landscape, and how it could have acted as physical reference point for organizing the positioning of all the associated Neolithic monuments within this area. For instance, the midpoint of the Major Cursus is precisely 9,090 ft (2.77 km) from the centers of the Durrington Walls Henge, Woodhenge, and two of the earthen long barrows.
The westernmost point of this cursus is 9,090 ft (2.77 km) away from Coneybury Hill and its associated henge, and the line between the two cuts through the center of Stonehenge. It is also 9,090 ft (2.77 km) from another earthen long barrow. Lastly, the westernmost point (of the Major Cursus) is one quarter of 9090 ft or 227.25 ft (69.2m) towards the midpoint of the Lesser Cursus.
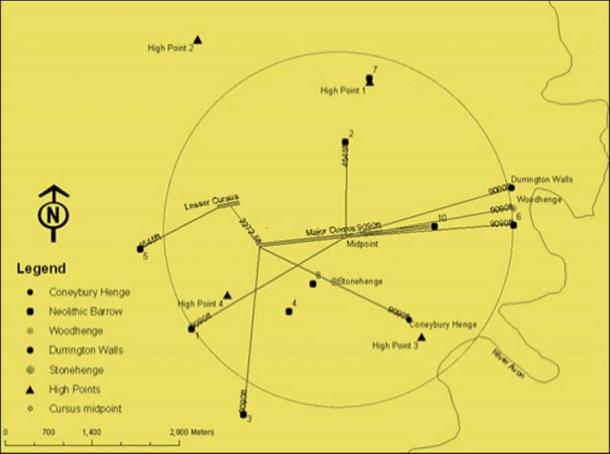
Fig.4. The 9,090 ft (2.77km) measurements associated with the Major Cursus at Stonehenge.
Matching Proportions at Stonehenge
The use of the 9,090 ft (2.77 km) measurement within the Stonehenge landscape is significant. An obvious question the reader may ask is whether the Proto-Druids made a length of rope nine thousand feet long to complete these measurements. It is certainly possible, and long lengths of ropes were both made and used by other ancient cultures for the practice of long-distance measuring (discussed below).
But let us break down this cumbersome length of 9,090 ft (2.77 km) into a more manageable “unit of measurement”, say 90 ft (27.4 m) long, and see how that unit relates to just three examples of the architectural dimensions at Stonehenge (Fig.5).
Firstly, the width of the Heel Stone, the famous outlying stone near Stonehenge that marks the summer solstice sunrise, is 9 ft (2.74 m) or one tenth of 90 ft (27.4 m). Secondly, the average length of an Outer Circle standing stone at Stonehenge is 18 ft (5.48 m) or twice the width of the Heel Stone; and the average depth for these stones, known as “sarsen stones”, was 4 ½ ft (1.37 m) or half of the 9 ft (2.74 m) width of the Heel Stone.
Thus, the sarsen circle stones originally stood 13 ½ ft (4.11 m) above ground level and 13 ½ ft (4.11 m) just happens to match the width of the circular Outer Ditch, which surrounds Stonehenge at a distance from the center of 180 ft (54.86 m), for a total diameter of 360 ft (109.73 m). The width of the earthen Inner Bank is 18 ft (5.48 m) wide, and the north-east entrance which interrupts both the ditch and bank is 36 ft (10.97 m) wide, that is one tenth of the diameter of the Outer Ditch or twice the width of the Inner Bank.
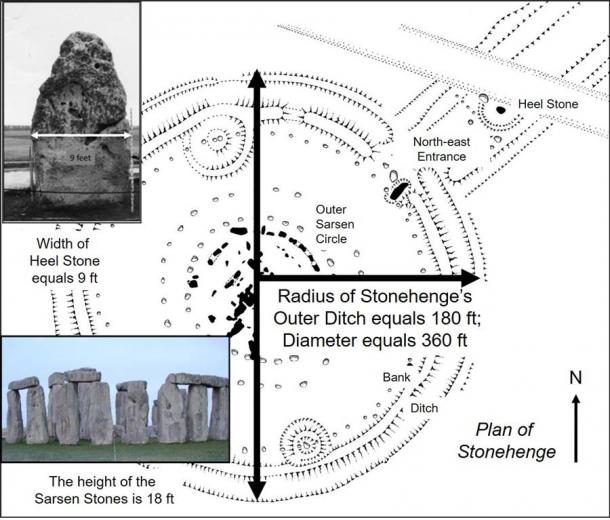
Fig.5. Measurements proportional to the 9,090 ft (2.77km) “natural measurement”.
In Harmony with the Landscape
What appears to be emerging from my mapping research is that during the British Neolithic there once existed a body of knowledge relating to the positioning of monuments in the landscape. This knowledge seems to have demanded an acknowledgement of the importance of the natural features in the landscape and their corresponding dimensions. Once this “knowledge” was understood, it was then translated into both a monument’s location and its inherent dimensions.
So why would the Proto-Druids behave in such a manner? The answer to this question is difficult, especially as the Neolithic communities were pre-literate. But is there any evidence for such a body of knowledge ever once existing within British pre-history? Maybe so, and the nearest explanation that can be offered here belongs to the late Iron Age druids.
Of course, these druids appeared almost two thousand years after the creation of Stonehenge and its ritual landscape. But we can comfortably place their appearance in British pre-history between 300 BC and 400 AD, when they are directly referred to in classical sources. I cannot find any earlier evidence from these written sources, even though a number of pre-historians are starting to think that the origins of the British Druidry might extend much further back in time than previously thought. For instance, Iron Age specialist Barry Cunliffe now considers the possibility that aspects of druidic knowledge could have originated as far back to the start of the Bronze Age, or 2,500 BC.
Undoubtedly, I believe that we are looking at some kind of specialist surveyor who possessed the ability to accurately measure on a large scale, in a way that would later be observed by the historical Greek and Roman classical authors. Obviously, for this to happen then the practice of their surveying would have had to continue across many generations (from the Neolithic, through to the Iron Age).
But if this practice of measuring did continue, then just how far had it evolved by the time that Julius Caesar, wrote about it in the first century BC when he was the Governor of Gaul? Although Caesar believed that Druidism originated in Britain, his writings focused on their counterparts in Gaul, where he described some tantalizing clues as to how effective they were at measuring:
“Besides this they (druids) have many discussions … as touching the size of the universe and of the earth” (De Bello Gallico, V1, 14).
- Was Orion the Heavenly Overlord of Stonehenge?
- Elevated Origins: Radical new theory suggests Stonehenge was base of an above-ground celestial altar
Incidentally, he also talks about large scale measuring, and that the Druids were apparently able to determine the precise center of Gaul:
“These Druids meet, at a certain time of the year, meet within the borders of the Carnutes, whose territory is reckoned as the center of Gaul” (De Bello Gallico, V1, 13).
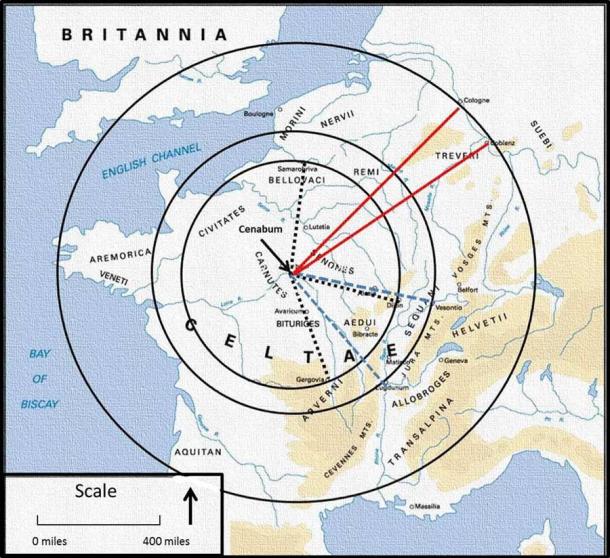
Fig. 6. Caesar never mentioned where the center of Gaul was, so I used the Iron Age town of Cenabum as its central point – and it produced some interesting results.
Calculating the geographical center of Ancient Gaul would have taken some measuring – but was not impossible (Fig. 6). And such large-scale measuring was not an isolated incident either. For example, writing nearly four centuries before Caesar, the Greek historian, Herodotus, provides us with a comparative analogy from Egypt:
“The length of Egypt itself along the coast is sixty reels of string … men who are poor in land measure their tracts in yards; men who are less poor in furlongs; and those who have a great deal in miles; and those who have a boundless quantity in reels of string. A mile is 8 furlongs and the reel – a measurement peculiar to Egypt equals 60 furlongs” (Book 2; Herodotus).
The degree of precision with which prehistoric monuments within the Stonehenge landscape were both constructed and positioned, using measurements from the natural environment, seems too deliberate to be simply dismissed as fortuitous. Moreover, the sheer scale of the measurements that had been performed around Stonehenge was staggering – but not impossible. Taking this further, the possibility that British druids in the late Iron Age could have measured and mapped out the entire British Mainland (like their counterparts did in Gaul) is intriguing to say the least!
Regarding Dr John Hill’s other work on Recumbent Stone Circles in Aberdeenshire:
I am visiting Aberdeenshire this August and will gladly present free, guided tours to any interested parties at the Loanhead of Daviot RSC on Tuesday 3rd August; at Tomnaverie RSC on Saturday 7th August and at the Easter Aquhorthies RSC on Saturday 10th August. Each event will commence from 13.00 onwards and will involve demonstrations of experimental archaeology with measured ropes. All, of course, subject to Covid restrictions being lifted by then.
You can make contact and find out more information about these events via his Facebook Group page – Friends of the Recumbent Stone Circles of Aberdeenshire
Dr. Hill’s book The Recumbent Stone Circles of Aberdeenshire: Archaeology, Design, Astronomy and Methods is available at: https://www.cambridgescholars.com/product/978-1-5275-6585-2
Top Image: Stonehenge and surrounding earthworks. Source: Darren Tennant / CC BY-NC-ND 2.0
By Dr John Hill
















Comments
Another example of how our remote ancestors were likely much more advanced in many areas than most contemporary “scientists” are willing to admit.
Very interesting. Thank you.