Euclid and the Birth of Geometry

It’s no secret that many of us are not too fond of mathematics and geometry, and that it is often too complex. But even so, it can be pretty mind-blowing to look back in history and discover the ancient thinkers who were way ahead of their time, and have come up with complex theorems, innovations, and discoveries in the field of mathematics. One such pioneer of scientific thought is Euclid, the Ancient Greek mathematician who flourished around 300 BC, and is considered the father of geometry.

Born in Alexandria, Egypt, his life and legacy have become the subject of fascination and reverence for scholars across centuries. What is more, his most important work, "Elements," not only laid the foundation for the study of geometry but also profoundly influenced the development of mathematics as a whole. Let’s learn more about this man who was ahead of his time.

• Imprisoned Murderer Solves Ancient Math Problem
• Megalithic Mathematics Revealed at the Cotswold Severn Long Barrows!

Euclid Laid the Foundations of Modern Geometry

Euclid's early life and education are not very well documented, leaving historians to piece together fragments of evidence and speculation to form a portrait of the man behind the mathematical legend. While precise details elude us, conjecture and inference provide tantalizing glimpses into his formative years. Modern historians generally agree that Euclid received his education in the Academy at Athens, the intellectual epicenter of the ancient world. It was in this vibrant city that the philosophical and mathematical ideas of luminaries such as Plato and his followers flourished. Some accounts suggest that Euclid may have been a student of Plato's Academy or studied under disciples of Plato, imbibing the philosophical underpinnings that would later inform his mathematical endeavors.

Another fascinating possibility is that Euclid's education was influenced by the Pythagorean school of thought. The Pythagoreans, renowned for their fascination with geometry and mathematical mysticism, exerted a profound influence on the intellectual milieu of ancient Greece. Euclid's emphasis on geometric abstraction and rigorous proof may reflect the Pythagorean penchant for mathematical purity and logical deduction. Regardless of the specifics of his formal education, it is evident that Euclid emerged from this crucible of intellectual learning with a deep appreciation for the power of deductive reasoning and logical argumentation. His mathematical prowess and pedagogical acumen would later find expression in his magnum opus, "Elements," a testament to his mastery of geometry and his ability to distill complex mathematical concepts into elegant, logical proofs.

In the absence of concrete biographical details, we are left to speculate on the influences that shaped Euclid's early life and education. Was he a natural talent? Or was he inspired by the greats that came before him? Whatever the case, what remains beyond doubt is the enduring legacy of his mathematical genius, which continues to inspire awe and admiration in mathematicians and scholars to this day. Euclid's journey from the obscurity of ancient times to the hallowed halls of mathematical immortality in the modern, scientific age serves as a testament to the power of human intellect and the timeless quest for knowledge and understanding.

• Sacred Geometry: Unlocking the Secret Structures of the Universe
• Mathematician Finds Pythagorean Triples on Ancient Babylonian Tablet

A 1650 painting of Euclid the mathematician. (Public Domain)

Euclid and the Birth of Geometry

The birth of geometry represents a pivotal moment in the evolution of human civilization, marking the dawn of systematic inquiry into the properties of space, shape, and form. While the origins of geometry can be traced back to the practical needs of ancient societies, such as land surveying and architectural design, its formalization as a mathematical discipline owes much to the intellectual endeavors of ancient Greek scholars like Thales, Pythagoras, and, most notably, Euclid. Geometry emerged organically from the observation and manipulation of physical objects in the natural world. Ancient civilizations, such as the Egyptians and Babylonians, developed rudimentary geometric concepts to facilitate tasks such as measuring land boundaries, constructing buildings, and predicting celestial events. These early geometric principles laid the groundwork for the more abstract and systematic approach to geometry that would later emerge in ancient Greece.

An illumination from a manuscript based on Adelard of Bath's translation of the Elements, 1309–1316; Adelard's is the oldest surviving translation of the Elements into Latin. (Public Domain)

The Greek concept of "geometries," meaning "earth measurement" or "land surveying," reflects the practical origins of geometry in the measurement and division of land. However, it was the Greek philosophers and mathematicians who sought to elevate geometry from a utilitarian craft to a rigorous intellectual pursuit. Thales of Miletus, often considered the first mathematician, is credited with introducing deductive reasoning and mathematical abstraction to geometry. His theorem regarding the properties of triangles formed by intersecting lines laid the foundation for subsequent geometric inquiry. The Pythagoreans, followers of the philosopher Pythagoras, further advanced the study of geometry, imbuing it with a sense of mathematical mysticism and philosophical significance. The Pythagorean theorem, which relates the lengths of the sides of a right triangle, remains one of the most famous results in geometry and a testament to the power of mathematical reasoning.

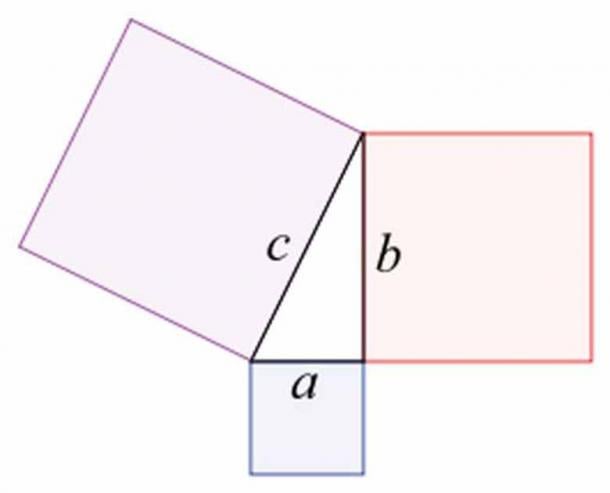
Illustration of the Pythagorean theorem. (CC BY SA 3.0)

However, it was Euclid who codified and systematized the disparate geometric principles of his predecessors into a comprehensive framework known as "Euclidean geometry." His magnum opus, "Elements," served as the definitive textbook on geometry for over two millennia, providing a rigorous foundation for the study of geometric principles, theorems, and proofs. Euclid's axiomatic approach to geometry, which relied on a small set of self-evident truths known as axioms, laid the groundwork for the deductive method that would become the hallmark of mathematical reasoning. By organizing geometric concepts into a logical and hierarchical structure, Euclid established geometry as a discipline grounded in rigorous proof and logical argumentation. The birth of geometry represents a triumph of human intellect and curiosity, transforming the practical concerns of ancient civilizations into a timeless intellectual pursuit.

A Man Who Etched His Name in History

Euclid's fundamental masterpiece is the book “Elements”, a thirteen-book treatise and his magnum opus. It was a monumental achievement in the history of mathematics, serving as the quintessential textbook on geometry for over two millennia. The treatise meticulously lays out the foundations of Euclidean geometry and sets the standard for mathematical exposition, logical reasoning, and rigorous proof. The thirteen books are as follows:

• Book I - Basics of Plane Geometry:
  This book lays out the fundamental concepts of geometry, including points, lines, angles, and planes. It introduces Euclid's famous five postulates, or axioms, which serve as the basis for all subsequent geometric reasoning.
• Book II - Geometric Algebra:
  Book II explores the properties of geometric figures such as triangles, parallelograms, and circles. It introduces concepts such as proportionality and similarity, laying the groundwork for more advanced geometric reasoning.
• Book III - Properties of Circles:
  This book is dedicated to the study of circles, including the properties of chords, tangents, and inscribed angles.
• Book IV - Regular Polyhedra:
  Book IV focuses on the properties of regular solids, such as the tetrahedron, cube, and dodecahedron. It introduces the concept of the Platonic solids and explores their geometric properties.
• Book V - Theory of Ratios:
  Book V delves into the theory of ratios and proportions, including the properties of geometric means and theorems related to proportionality.
• Book VI - Similar Figures:
  This book explores the properties of similar figures and the relationships between corresponding sides and angles.
• Book VII - Number Theory:
  Book VII introduces the theory of numbers, including the properties of primes, divisibility, and the algorithm for finding the greatest common divisor.
• Book VIII - Arithmetic and Geometric Progressions:
  Book VIII examines arithmetic and geometric progressions, including the properties of sums of terms and theorems related to these sequences.
• Book IX - Number Theory Continued:
  This book continues the exploration of number theory, including the properties of perfect numbers, prime factorization, and the Euclidean algorithm.
• Book X - Irrational Numbers and Geometric Algebra:
  Book X introduces the concept of irrational numbers and explores their relationship to geometric quantities such as lengths and areas.
• Book XI - Solid Geometry:
  Book XI focuses on solid geometry, including the properties of cones, cylinders, and spheres. It also explores the relationship between the volumes and surface areas of these solids.
• Book XII - Dodecahedron and Its Properties:
  This book is dedicated to the study of the dodecahedron, one of the five Platonic solids, and its geometric properties.
• Book XIII - Archimedes' Method:
  The final book of the "Elements" is a compilation of results attributed to the mathematician Archimedes, including the measurement of circles and the calculation of volumes of various solids.

Euclid's "Elements" is renowned for its systematic organization, logical rigor, and emphasis on deductive reasoning. Each proposition is stated clearly and precisely, followed by a rigorous proof that relies on previously established results. Euclid's axiomatic method, which begins with a small set of self-evident truths and derives further results through logical deduction, sets the standard for mathematical exposition. The influence of Euclid's magnum opus extends far beyond the realm of geometry, shaping the course of mathematical inquiry for centuries. Its emphasis on logical reasoning, rigorous proof, and systematic organization serves as a model for mathematical exposition in fields ranging from algebra and number theory to calculus and beyond.

Euclid is considered the father of geometry. Elements, a fragment of which is shown here, is one of the most influential works in the history of mathematics. (Public Domain)

Centuries Ahead of His Time

Euclid's contributions to mathematics extend far beyond the realm of geometry, encompassing a wide range of mathematical disciplines and laying the groundwork for many fundamental concepts and methods that continue to shape the field to this day. While he is most renowned for his work in geometry, particularly his magnum opus, Euclid's influence transcends this single discipline, touching upon number theory, algebra, and mathematical logic. For example, Euclid's "Elements" introduced the axiomatic method to mathematical inquiry, laying the foundation for the deductive approach that would become the hallmark of mathematical reasoning. By starting with a set of axioms, or self-evident truths, and deriving further results through logical deduction, Euclid established a rigorous framework for mathematical proof that continues to influence the field to this day. The axiomatic method provides a solid foundation for building mathematical theories and ensures the clarity and precision of mathematical arguments.

A page with marginalia from the first printed edition of Euclid's Elements, printed by Erhard Ratdolt in 1482. (Erhard Ratdolt/CC BY-SA 4.0)

His influence can also be seen in the development of algebraic methods. His work on proportions and ratios laid the groundwork for algebraic reasoning, particularly in the context of solving equations and manipulating algebraic expressions. Euclidean geometry provided a geometric interpretation for algebraic concepts, and his emphasis on logical reasoning and rigorous proof set the stage for the development of modern algebraic structures and techniques.

Furthermore, he also made significant contributions to number theory, particularly in the theory of primes. Book VII of "Elements" is dedicated to the study of number theory, including properties of primes, divisibility, and the algorithm for finding the greatest common divisor. Euclid's algorithm for finding the greatest common divisor of two numbers remains a fundamental tool in number theory and has applications in fields such as cryptography and computer science.

Loved by Students Across the World

In the end, it is incredible how one man’s contributions to mathematics have had a profound and lasting impact on the field, shaping the course of mathematical inquiry for centuries. Euclid’s emphasis on logical reasoning, rigorous proof, and systematic organization set the standard for mathematical exposition and laid the groundwork for many fundamental concepts and methods in mathematics. From his axiomatic method to his insights into geometry, number theory, and algebra, Euclid's legacy continues to inspire and inform mathematicians and scholars to this day, reminding us of the timeless beauty and elegance of mathematical truth.

Top image: Left, Painting of Euclid. Right, A page first printed edition of Euclid's Elements.           Source: Fondazione Cariplo/CC BY-SA 3.0; Erhard Ratdolt /CC BY-SA 4.0

By Aleksa Vučković